While attempting to convert floats precisely to Decimals the other day I was caught out by the fact that Python 2.6’s print function defers to whatever the underlying C compiler’s printf function does. This meant that on Linux I got one result when I asked for ‘%.31f’ % math.pi, and on Windows – something completely different. This lack of portability is a pain, and I had to work around it.

‘Why not use repr ?’ I hear you ask. Because it doesn’t give you a precise representation – witness:

>>> 1.1 * 1.1
1.2100000000000002
>>> from decimal import Decimal
>>> Decimal( repr(1.1) ) * Decimal( repr(1.1) )
Decimal('1.21')
>>> Decimal( repr( 1.1 * 1.1 ) )
Decimal('1.2100000000000002')

As you note, repr provides the shortest representation that you are likely to want within the granularity of a floating point number, not the exact midpoint value. Which is what I wanted

There are various very good reasons for Decimal not supporting direct conversion, but if the only way in is float to string conversion that varies by platform, then it’s kind of crappy. Note this has been fixed in later versions of Python (2.7 and 3.x support from_float) but for various reasons I’m stuck with 2.6 for now.

As it turns out there are two ways to do it: an easy way, and a hard way.

The Easy Way – Integer Ratios

import decimal

def floatToDecimalViaRatio( f ):
     '''Given a floating point number, 
        return the exact representation of that number as a decimal '''
     top, bottom = f.as_integer_ratio()
     return decimal.Decimal( top ) / decimal.Decimal( bottom )

Obviously this doesn’t handle NaN, +Inf, -Inf but it gets the job done. There is one minor issue with it if you are operating inside hugely precise Decimal contexts: Divide is a bit slow.

Besides this was a bit boring. Is it possible to pull a float apart and get at the mantissa and exponent directly ?

The Hard Way – Extracting Mantissa and Exponent

In C this would be a straightforward cast to a 64 bit long and a bit of shifting. In Python you have to cheat. One way I’ve seen to do this is using struct.pack and unpack. But testing this I found to be very slow.

So after experimenting a bit, I came up with using the C interface library to do a cast:

mantissa_mask = (2 ** 52) - 1
exponent_mask = ((2 ** 63) - 1) - mantissa_mask
sign_mask = (2 ** 63)

def float_to_mantissa_exponent_negative( f ):
    val = cast((c_double * 1)(f), POINTER(c_ulonglong)).contents.value
    exponent = ((val & exponent_mask) >> 52L) - 1023
    mantissa = val & mantissa_mask
    negative = bool(val & sign_mask)
    return exponent, mantissa, negative

Now the first line casts the 64bit floating point value (as an array of c_double of size 1) to a c_longlong, and then unpacks the contents into val.

The rest is some straightforward masking and shifting. The minus 1023 comes from the fact that the exponent is stored unsigned, and makes for easier comparisons in hardware.

Now we have the various bits of the floating point value – can we bring it all together ?

import ctypes
import decimal

zero = decimal.Decimal( 0 )
two  = decimal.Decimal( 2 )
twofiftytwo = two ** decimal.Decimal( 52 )

mantissaMSB  = 2L ** 52L
mantissaMask = ( 2L ** 52L ) - 1L
exponentMask = ( ( 2L ** 63L ) - 1L ) - mantissaMask
signMask = 2L ** 63L

# @context_memo - add memoization here - don't forget to include the decimal.context into the args...
def _decimal_exponent(exponent, negative):
    """ When passed an exponent, returns the corresponding decimal value, divided by 2 ** 52
    """
    res = (two ** decimal.Decimal(exponent)) / two_pow_fifty_two
    if negative:
        return negative_one * res
    return res

def float_to_decimal(f):
    """ Convert a passed floating point number to a Decimal, by directly accessing the mantissa and exponent of
     the floating point value. Depends on decimal.context to provide sufficient precision for this operation """
    val = cast((c_double * 1)(f), POINTER(c_ulonglong)).contents.value  # c-style cast of float to long
    exponent = ((val & exponent_mask) >> 52L) - 1023
    mantissa = val & mantissa_mask
    full_mantissa = mantissa + mantissa_msb  # 1.1 instead of .1
    negative = bool(val & sign_mask)

    if exponent not in (1024, -1023):  # Most common case
        if exponent > 55:  # No fractional part - rely on Pythons arbitrary length longs and shifting
            if negative:
                return decimal.Decimal(-(full_mantissa << (exponent - 52)))
            else:
                return decimal.Decimal(full_mantissa << (exponent - 52))
        else:
            return decimal.Decimal(full_mantissa) * _decimal_exponent(exponent, negative)
    elif exponent == 1024:  # (i.e. all ones: +/- inf, NaN)
        return decimal.Decimal(str(f))
    elif exponent == -1023 and mantissa == 0:
        return zero  # No negative zero
    elif exponent == -1023:
        # Denormal number, no leading one, special case mantissa 0.1 or 0.01 instead of 1.1
        return decimal.Decimal(mantissa) * _decimal_exponent(-1022, negative)
    else:
        raise RuntimeError('Unexpected error during conversion')

So why on earth would you want to do it the hard way ? Given the extra complexity ?

Two reasons: It’s slightly faster on typical cases, and where you are operating inside a decimal context with extreme precision (>50 digits), it may be much much faster.

So why is it faster? In essence the ‘hard way’ spends most of it’s time bit shifting Native Longs, and then right at the end it does a single Decimal multiply. The exponent part is likely to have been memoized, so is already constructed and costs nothing.

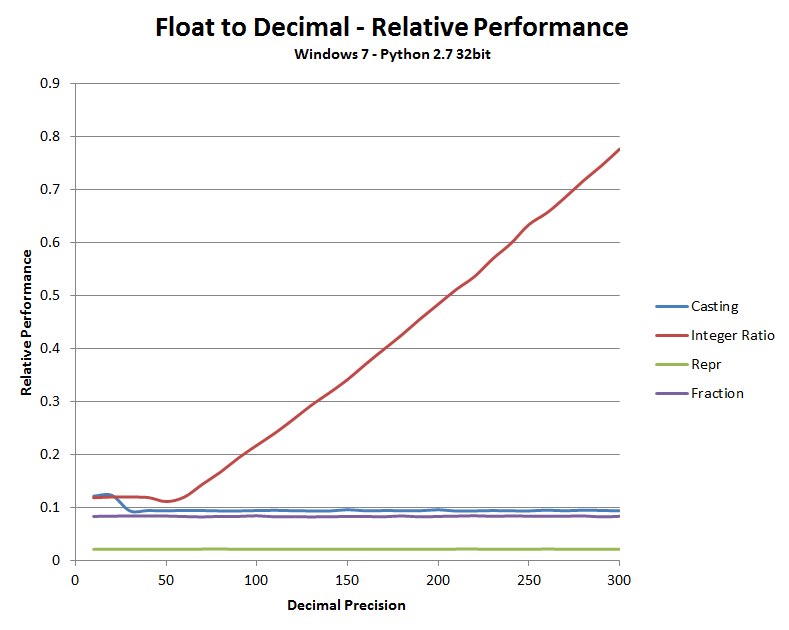
Comparing Performance of Float To Python Decimal Techniques

I wrote a simple benchmark that converts math.e and math.pi two hundred times in a loop to compare the methods. As you can see Repr is very fast – but as discussed isn’t suitable for my needs. Using Fraction instead of decimal is comparable to the casting method (it uses as_integer_ratio under the covers).

Now don’t get too excited. There is some clever magic in the new from_float factory method that makes it faster still, but I was quite impressed that I managed to come close in pure Python.

A performance comparison of techniques to convert a floating point number to a Python Decimal. from_float is comparable to repr (but slightly slower)